Signed-digit representation
| Numeral systems by culture | |
|---|---|
| Hindu-Arabic numerals | |
| Western Arabic (Hindu numerals) Eastern Arabic Indian family Tamil |
Burmese Khmer Lao Mongolian Thai |
| East Asian numerals | |
| Chinese Japanese Suzhou |
Korean Vietnamese Counting rods |
| Alphabetic numerals | |
| Abjad Armenian Āryabhaṭa Cyrillic |
Ge'ez Greek Georgian Hebrew |
| Other systems | |
| Aegean Attic Babylonian Brahmi Egyptian Etruscan Inuit |
Kharosthi Mayan Quipu Roman Sumerian Urnfield |
| List of numeral system topics | |
| Positional systems by base | |
| Decimal (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 20, 24, 30, 36, 60, 64 | |
| Non-positional system | |
| Unary numeral system (Base 1) | |
| List of numeral systems | |
Signed-digit representation of numbers indicates that digits can be prefixed with a − (minus) sign to indicate that they are negative.
Signed-digit representation can be used in low-level software and hardware to accomplish fast addition of integers because it can eliminate carries.[1] In the binary numeral system one special case of signed-digit representation is the non-adjacent form which can offer speed benefits with minimal space overhead.
Contents |
Balanced form
In balanced form, the digits are drawn from a range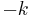 
to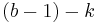 
, where typically 
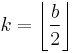. For balanced forms, odd base numbers are advantageous. With an odd base number, truncation and rounding become the same operation, and all the digits except 0 are used in both positive and negative form.
A notable example is balanced ternary, where the base is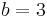 
, and the numerals have the values −1, 0 and +1 (rather than 0, 1, and 2 as in the standard ternary numeral system). Balanced ternary uses the minimum number of digits in a balanced form. Balanced decimal uses digits from −5 to +4. Balanced base nine, with digits from −4 to +4 provides the advantages of an odd-base balanced form with a similar number of digits, and is easy to convert to and from balanced ternary.
Other notable examples include Booth encoding and non-adjacent form, both of which use a base of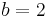 
, and both of which use numerals with the values −1, 0, and +1 (rather than 0 and 1 as in the standard binary numeral system).
Non-unique representations
Note that signed-digit representation is not necessarily unique. For instance:
- (0 1 1 1)2 = 4 + 2 + 1 = 7
- (1 0 −1 1)2 = 8 − 2 + 1 = 7
- (1 −1 1 1)2 = 8 − 4 + 2 + 1 = 7
- (1 0 0 −1)2 = 8 − 1 = 7
The non-adjacent form does guarantee a unique representation for every integer value, as do balanced forms.
When representations are extended to fractional numbers, uniqueness is lost for non-adjacent and balanced forms; for example,
- (0 . (1 0) …)NAF = ⅔ = (1 . (0 −1) …)NAF
and
- (0 . 4 4 4 …)(10bal) = 4⁄9 = (1 . -5 -5 -5 …)(10bal)
Such examples can be shown to exist by considering the greatest and smallest possible representations with integral parts 0 and 1 respectively, and then noting that they are equal. (Indeed, this works with any integral-base system.)